Rozwiązywanie równań wielomianowych na maturze

Wprowadzenie

Zadanie polegające na rozwiązaniu równania wielomianowego to stały punkt matury w nowej formule. Za takie zadanie można zdobyć przeważnie 2 punkty czyli 4 punkty procentowe na maturze z matematyki. Zadanie tego typu pojawiło się na maturach:

Matura próbna grudzień 2024
Matura poprawkowa sierpień 2024
Matura dodatkowa sierpień 2024
Matura maj 2024
Matura próbna grudzień 2023
Matura poprawkowa sierpień 2023
Matura dodatkowa czerwiec 2023
Matura maj 2023

Jest to klasyczny przykład "pewniaka maturalnego" na maturze z matematyki. Warto nauczyć się rozwiązywać ten typ zadania. Schemat rozwiązania jest powtarzany i pozwala zdobyć pewne punkty na maturze.

Przypomnienie wiadomości

Do rozwiązania równania wielomianowego potrzebujemy kilku podstawowych wiedomości na temat rozwiązywania równań. Podstawą jest zasada, że jeśli iloczyn dwóch nawiasów jest równy zero, to któryś z nich musi być równy zero. Mając równanie

(x-1)(x-2)=0

rozwiązujemy jest przez przyrównaniu nawiasów do zera :

x-1=0

lub

x-2=0

przenosimy liczby na drugą stronę i otrzymujemy rozwiązanie

x_{1}=1, x_{2}=2.

Przyda nam się też umiejętność sprawnego rozwiązywania niepełnego równania kwadratowego. Jest to takie równanie, w którym jeden ze współczynników

b,c

jest równy

0

. Takie równanie można rozwiązać klasycznie licząc

\Delta

i dalej wyznaczając ze wzorów

x_{1}, x_{2}

. Warto jednak rozwiązywać takie równania szybko i sprawnie. Jeśli

b=0

c>0

to równanie może wyglądać tak

x^{2}+1=0

Takie równanie nie ma rozwiązania w liczbach rzeczywistych. Jeśli

b=0

c=0

to mamy równanie

x^{2}=0

które ma rozwiązanie

x=0

. Jeśli

c<0

to nasze równanie może wyglądać tak

x^{2}-3=0

Do jego rozwiązania możemy zastosować wzór skróconego mnożenia

a^{2}-b^{2}=(a-b)(a+b)

. który przekształci lewą stroną równanie

(x-\sqrt{3})(x+\sqrt{3})=0

Teraz możemy odczytać

x_{1}=\sqrt{3}

x_{2}=-\sqrt{3}

korzystając z regułu iloczynu dwóch nawiasów. Jeśli współczynnik

c=0

b \neq 0

to równanie może wyglądać tak

x^{2}-2x=0

Wyciągając teraz

x

przed nawias dostaniemy

x(x-2)=0

Odczytujemy dalej rozwiązania

x=0

x=2

Analiza zadania i schemat rozwiązania

Poddamy dokładniejszej analizie zadanie z majowej matury 2024. Wyglądało ono tak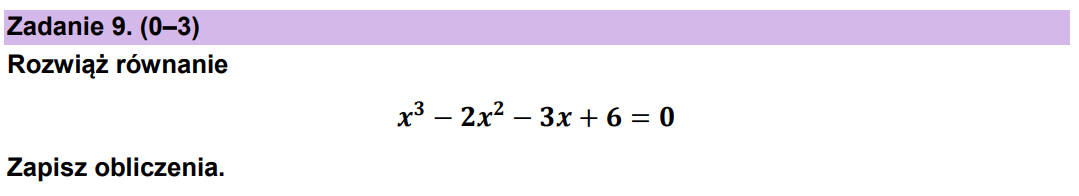

Za zadanie można było otrzymać 3 punkty czyli 6 punktów procentowych. Schemat rozwiązania jest następujący

Przenosimy wszystkie wyrazy na lewą stronę, tak aby po prawej stronie było $0$
Wyciągamy $x^{2}$ przed nawias z pierwszych dwóch składników
Wyciągamy stałą z dwóch ostatnich składników tak, żeby nawias powtórzył się w pierwszym nawiasem
Wyciągamy nawias z dwóch składników i dostajemy równanie $()()=0$
Przyrównujemy każdy z nawiasów do $0$ i rozwiązujemy równanie.

W tym zadaniu wszystkie składniki są po lewej stronie, dlatego pierwszy krok pomijamy. W drugim kroku wyciągamy

x^{2}

przed nawias

x^{2}(x-2)-3x+6=0

W trzecim kroku wyciągamy

-3

przed nawias. Dlaczegu akurat

-3

? Spowoduje to powstanie nawiasu

(x-2)

który powstał z pierwszych dwóch składników równania.

x^{2}(x-2)-3(x-2)=0

W czwartym kroku wyciągamy wspólny nawias z dwóch składników

(x-2)(x^2-3)=0

W piątym kroku przyrównujemy nawiasy do zera

(x-2)=0 \rightarrow x_{1}=2

x^2-3=0 \rightarrow (x-\sqrt{3})(x+\sqrt{3})=0

Odczytujemy rozwiązanie

x_{2}=\sqrt{3}, \ x_{3}=-\sqrt{3}

Odpowiedź:

x_{1}=2, x_{2}=\sqrt{3}, \ x_{3}=-\sqrt{3}

Matura poprawkowa sierpień 2024

Zadanie numer 10 z czerwca 2024 brzmiało tak: Rozwiąż równanie

4x^{3}-12x^{2}-x+3=0

Zadanie rozwiązujemy zgodnie z krokami naszego schematu. Wszystkie wyraz są po lewej stronie równania. W drugim kroku wyciągamy

4x^{2}

z dwóch pierwszych wyrazów

4x^{2}(x-3)-x+3=0

Wyciągneliśmy

4x^{2}

przed nawias tak, aby w nawiasie zostało

(x-3)

. To pozwoli nam bezproblemowo zapisać drugi nawias. Gdybyśmy wyciągneli samo

x^{2}

przy drugim nawiasie musielibyśmy wyciągnąć ułamek - pokażemy i to rozwiązanie. Zapisujemy drugi nawias i wyciągamy wspólny nawias

4x^{2}(x-3)-(x-3)=0

(x-3)(4x^{2}-1)=0

Mamy równanie w postaci

()()=0

, to chcieliśmy otrzymać. Pokażemy teraz drugi sposób wyciągania przed nawias

x^{2}(4x-12)-x+3=0

x^{2}(4x-12)-\frac{1}{4}(4x-12)=0

Zauważmy, że

\frac{1}{4}(4x-12) = x-3

. Mamy dalej

(4x-12)(x^{2}-\frac{1}{4})=0

Możemy teraz wyciągnąć

4

z pierwszego nawiasu i wciągnąć do drugiego

4(x-3)(x^{2}-\frac{1}{4})=0

(x-3)(4x^{2}-1)=0

Otrzymujemy taką samą postać równania jak w pierwszym sposobie. Przechodzimy do następnego kroku i przyrównujemy nawiasy do

0

x-3=0 \rightarrow x_{1}=3

4x^{2}-1=0

(2x-1)(2x+1)=0

2x-1=0 \rightarrow 2x=1 \rightarrow x_{2}=\frac{1}{2}

2x+1=0 \rightarrow 2x=-1 \rightarrow x_{3}=-\frac{1}{2}

Rozwiązania równania to

x_{1}=3,x_{2}=\frac{1}{2}, x_{3}=-\frac{1}{2}