Przekształcenia trygonometryczne

Trójkąt prostokątny ABC

Wprowadzenie

Zadanie dotyczące przekształcenia wyrażeń trygonometrycznych jest często występującym zadaniem na maturze. W ostatnim czasie pojawiło się na maturach

  1. Matura próbna grudzień 2024
  2. Matura poprawkowa sierpień 2024
  3. Matura dodatkowa czerwiec 2024
  4. Matura maj 2024
  5. Matura próbna grudzień 2023
  6. Matura poprawkowa sierpień 2023
  7. Matura dodatkowa czerwiec 2023
  8. Matura maj 2023
  9. Matura próbna grudzień 2022
  10. Matura próbna wrzesień 2022
Jest to klasyczny przykład "pewniaka maturalnego" na maturze z matematyki. Warto nauczyć się rozwiązywać ten typ zadania. Schemat rozwiązania jest powtarzany i pozwala zdobyć pewne punkty na maturze. Jeden punkt na maturze to dwa punkty procentowe.

Matura próbna wrzesień 2022

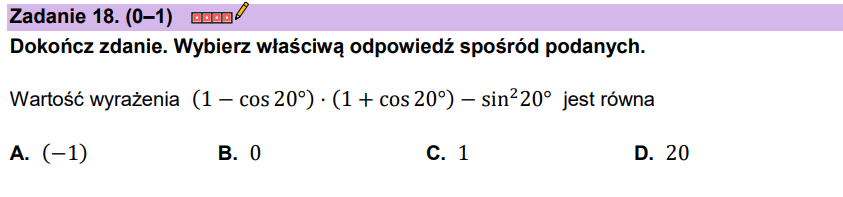Trójkąt prostokątny ABCW tym zadaniu narzuca się wzór (a−b)(a+b)=a2−b2(a-b)(a+b)=a^{2}-b^{2} dla a=1a=1 i b=cos⁡20∘b=\cos{20^{\circ}}. Po jego zastosowaniu dostajemy
(1−cos⁡20∘)(1+cos⁡20∘)=1−cos⁡220∘(1-\cos{20^{\circ}})(1+\cos{20^{\circ}})=1-\cos^{2}{20^{\circ}}
Nasze wyrażenie z treści zadania wygląda teraz tak
(1−cos⁡20∘)(1+cos⁡20∘)−sin⁡220∘=1−cos⁡220∘−sin⁡220∘(1-\cos{20^{\circ}})(1+\cos{20^{\circ}})-\sin^{2}{20^{\circ}}=1-\cos^{2}{20^{\circ}} - \sin^{2}{20^{\circ}}
Widzimy tutaj, że mamym kwadraty sinusa i kosinusa, możemy więc zastosować dobrze znaną jedynkę trygonometryczną
1−cos⁡220∘−sin⁡220∘=1−(cos⁡220∘+sin⁡220∘)=1−1=01-\cos^{2}{20^{\circ}} - \sin^{2}{20^{\circ}}=1-(\cos^{2}{20^{\circ}} + \sin^{2}{20^{\circ}})=1-1=0
Otrzymaliśmy 0 i zaznaczamy odpowiedź B. Jest to zadanie zamknięte, możemy je spróbować rozwiązać trochę na skróty nie wykonując przekształceń. Taka technika jest możliwa tylko dla zadań zamkniętych i nie zawsze jest skuteczna. Z tablic odczytujemy, że cos⁡20∘=0,9397\cos{20^{\circ}}=0,9397 oraz cos⁡20∘=0,3420\cos{20^{\circ}}=0,3420. Obliczamy dalej z użyciem kalkulatora
1−cos⁡20∘=0,06031 - \cos{20^{\circ}} = 0,0603
1+cos⁡20∘=1,93971 + \cos{20^{\circ}} = 1,9397
(1−cos⁡20∘)(1+cos⁡20∘)=0,0603⋅1,9397=0,1170(1-\cos{20^{\circ}})(1+\cos{20^{\circ}}) = 0,0603 \cdot 1,9397 = 0,1170
sin⁡220∘=0,3420⋅0,3420=0.1170\sin^{2}{20^{\circ}} = 0,3420 \cdot 0,3420 =0.1170
(1−cos⁡20∘)(1+cos⁡20∘)−sin⁡220∘=0,1170−0,1170=0(1-\cos{20^{\circ}})(1+\cos{20^{\circ}}) - \sin^{2}{20^{\circ}} =0,1170 - 0,1170=0
Zaznaczamy odpowiedź B.

Matura próbna grudzień 2022

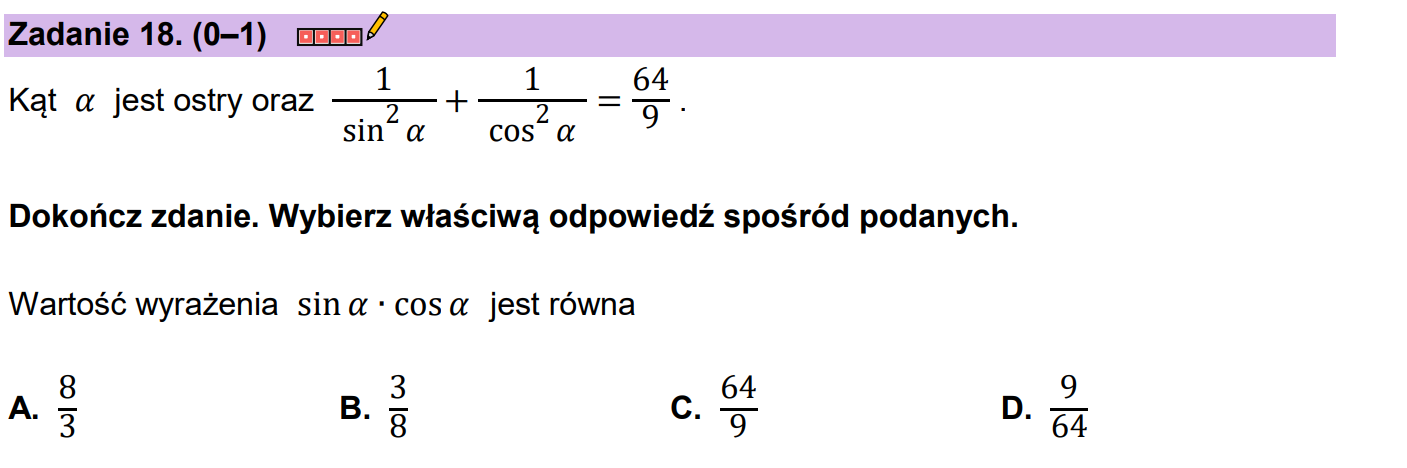Trójkąt prostokątny ABCW równaniu po lewej stronie mamy sumę dwóch ułamków. W mianownikach mamy funkcje trygonometryczne w kwadracie - prawdopodobnie będziemy mogli skorzystać z jedynki trygonometrycznej. Przekształcmy lewą stronę równania
1sin⁡2α+1cos⁡2α=cos2αcos2α⋅sin⁡2α+sin⁡2αsin⁡2α⋅cos⁡2α=cos⁡2α+sin⁡2αsin⁡2α⋅cos⁡2α=1sin⁡2α⋅cos⁡2α\frac{1}{\sin^{2}{\alpha}}+\frac{1}{\cos^{2}{\alpha}}= \frac{cos^{2}{\alpha}}{cos^{2}{\alpha} \cdot \sin^{2}{\alpha}}+\frac{\sin^{2}{\alpha}}{\sin^{2}{\alpha} \cdot \cos^{2}{\alpha}}= \frac{\cos^{2}{\alpha} +\sin^{2}{\alpha} }{\sin^{2}{\alpha} \cdot \cos^{2}{\alpha}}=\frac{1}{\sin^{2}{\alpha} \cdot \cos^{2}{\alpha}}
Podczas przekształcania lewej strony równania sprowadziliśmy ułamki do wspólnego mianownika i zastosowaliśmy jedynkę trygonometryczną. W zadaniu pytają na o wartość wyrażenia sin⁡αcos⁡α\sin{\alpha}\cos{\alpha}. Szukana wartość znajduje się w naszym mianowniku, tylko podniesiona do kwadratu. Wyznaczmy ją z naszego równania
1sin⁡2α⋅cos⁡2α=649\frac{1}{\sin^{2}{\alpha} \cdot \cos^{2}{\alpha}} = \frac{64}{9}
Po wymnożeniu na krzyż
9=64⋅sin⁡2α⋅cos⁡2α 9 = 64 \cdot\sin^{2}{\alpha} \cdot \cos^{2}{\alpha}
sin⁡2α⋅cos⁡2α=964\sin^{2}{\alpha} \cdot \cos^{2}{\alpha} = \frac{9}{64}
Zapisujemy to z użyciem kwadratów
(sin⁡α⋅cos⁡α)2=(38)2(\sin{\alpha} \cdot \cos{\alpha})^{2} = (\frac{3}{8})^{2}
W treści zadania została podana informacje, że kąt α\alpha jest ostry, co oznacza, że jego sinus i kosinus są dodatnie. To oznacz, że ich iloczyn również jest dodatni. Wiedząc to, obliczamy dalej
sin⁡α⋅cos⁡α=38\sin{\alpha} \cdot \cos{\alpha} = \frac{3}{8}
α\alphaWynik ujemny odrzuciliśmy, uzasadniając wcześniej, że dla kąta ostrego α\alpha wyrażeniesin⁡α⋅cos⁡α\sin{\alpha} \cdot \cos{\alpha} jest dodatnie. Zaznaczamy odpowiedź B.

Matura dodatkowa czerwiec 2023

Trójkąt prostokątny ABCW każdym składniku wyrażenia które musimy przekształcić znajduje się czynnikcos⁡α\cos{\alpha} spróbujmy więc go wyciągnąc przed nawias.
cosα−cosα⋅sin⁡2α=cos⁡α(1−sin⁡2α)cos{\alpha}-cos{\alpha} \cdot \sin^{2}{\alpha}= \cos{\alpha}(1-\sin^{2}{\alpha})
Wyrażenie 1−sin⁡2α1-\sin^{2}{\alpha} możemy wyznaczyć z jedynki trygonometrycznej
sin⁡2α+cos⁡2α=1→cos2α=1−sin⁡2α \sin^{2}{\alpha}+\cos^{2}{\alpha}=1 \rightarrow cos^{2}{\alpha}=1-\sin^{2}{\alpha}
Wracąj do wyrażenia z zadania
cos⁡α(1−sin⁡2α)=cos⁡α⋅cos⁡2α=cos⁡3α \cos{\alpha}(1-\sin^{2}{\alpha}) = \cos{\alpha} \cdot \cos^{2}{\alpha} = \cos^{3}{\alpha}
Zaznaczamy odpowiedź A.

Matura maj 2023

Trójkąt prostokątny ABC

W wyrażeniu sin⁡4α+sin⁡2α⋅cos⁡2α\sin^4 \alpha + \sin^2 \alpha \cdot \cos^2 \alpha możemy wyciągnąć wspólny czynnik sin⁡2α\sin^{2}{\alpha} przed nawias:

sin⁡4α+sin⁡2α⋅cos⁡2α=sin⁡2α(sin⁡2α+cos⁡2α)\sin^4 \alpha + \sin^2 \alpha \cdot \cos^2 \alpha = \sin^2 \alpha (\sin^2 \alpha + \cos^2 \alpha)

Następnie korzystamy z jedynki trygonometrycznej:

sin⁡2α+cos⁡2α=1\sin^2 \alpha + \cos^2 \alpha = 1

Wstawiając to do poprzedniego wyrażenia, otrzymujemy:

sin⁡2α(sin⁡2α+cos⁡2α)=sin⁡2α⋅1=sin⁡2α\sin^2 \alpha (\sin^2 \alpha + \cos^2 \alpha) = \sin^2 \alpha \cdot 1 = \sin^2 \alpha

Zatem wyrażenie sin⁡4α+sin⁡2α⋅cos⁡2α\sin^4 \alpha + \sin^2 \alpha \cdot \cos^2 \alpha jest równe

sin⁡4α+sin⁡2α⋅cos⁡2α=sin⁡2α\sin^4 \alpha + \sin^2 \alpha \cdot \cos^2 \alpha = \sin^{2}{\alpha}

Prawidłowa odpowiedź to A. .