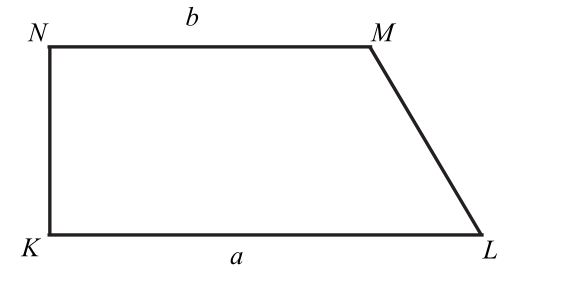
Dany jest trapez prostokątny KLMNKLMN, którego podstawy mają długości ∣KL∣=a|KL| = a, ∣MN∣=b, a>b|MN| = b, \, a > b. Kąt KLMKLM ma miarę 60∘60^\circ. Długość ramienia LMLM tego trapezu jest równa:

ODPOWIEDŹ A: a−ba - b

ODPOWIEDŹ B: 2(a−b)2(a - b)

ODPOWIEDŹ C: a+12ba + \frac{1}{2}b

ODPOWIEDŹ D: a+b2\frac{a+b}{2}

Krok 1: Analiza trapezu

Trapez KLMNKLMN jest prostokątny, więc ramię LMLM jest prostopadłe do podstaw. Kąt KLMKLM ma miarę 60∘60^\circ.

Krok 2: Obliczenie długości ramienia

Różnica długości podstaw wynosi a−ba - b. Ponieważ kąt KLMKLM wynosi 60∘60^\circ, możemy użyć funkcji trygonometrycznych do obliczenia długości ramienia LMLM:

cos⁡(60∘)=przyległaprzeciwprostokątna\cos(60^\circ) = \frac{\text{przyległa}}{\text{przeciwprostokątna}}

Podstawiamy wartości:

cos⁡(60∘)=a−b∣LM∣\cos(60^\circ) = \frac{a - b}{|LM|}

Wiemy, że cos⁡(60∘)=12\cos(60^\circ) = \frac{1}{2}, więc:

12=a−b∣LM∣\frac{1}{2} = \frac{a - b}{|LM|}

Rozwiązujemy równanie:

∣LM∣=2(a−b)|LM| = 2(a - b)

Odpowiedź

Długość ramienia LMLM wynosi 2(a−b)2(a - b) (odpowiedź B).