Funkcja

g

jest określona wzorem

g(x) = f(x) - 2

dla

x \in (-6, 5)

. Wskaż zdanie prawdziwe:

ODPOWIEDŹ A: Liczba $f(2) + g(2)$ jest równa $-2$ .

ODPOWIEDŹ B: Zbiory wartości funkcji $f$ i $g$ są równe.

ODPOWIEDŹ C: Funkcje $f$ i $g$ mają te same miejsca zerowe.

ODPOWIEDŹ D: Punkt $P = (0, -2)$ należy do wykresów funkcji $f$ i $g$ .

Krok 1: Analiza odpowiedzi A

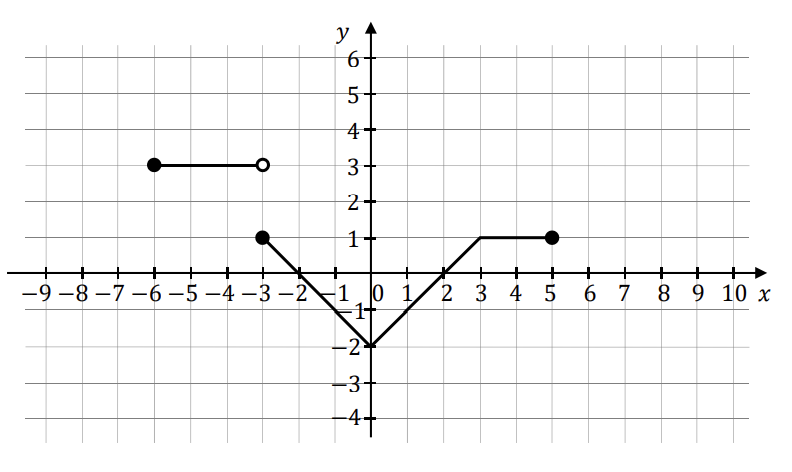
Z definicji funkcji $g(x) = f(x) - 2$ , mamy:

f(2) + g(2) = f(2) + (f(2) - 2) = 2f(2) - 2

Z wykresu możemy odczytać, że $f(2) = 0$ , musi zachodzić więc:

2f(2) - 2 = 2\cdot 0 - 2 = -2

Zatem odpowiedź A jest poprawna

Krok 2: Analiza odpowiedzi B

Zbiór wartości funkcji $g$ jest przesunięty o 2 w dół względem zbioru wartości funkcji $f$ , więc zbiory te nie są równe. Odpowiedź B jest fałszywa.

Krok 3: Analiza odpowiedzi C

Miejsca zerowe funkcji $g$ to takie $x$ , że $g(x) = 0$ , czyli $f(x) - 2 = 0 \Rightarrow f(x) = 2$ . Miejsca zerowe funkcji $f$ to $f(x) = 0$ . Zatem funkcje $f$ i $g$ nie mają tych samych miejsc zerowych. Odpowiedź C jest fałszywa.

Krok 4: Analiza odpowiedzi D

Punkt $P = (0, -2)$ należy do wykresu funkcji $g$ , jeśli $g(0) = -2$ . Z definicji:

g(0) = f(0) - 2

Aby $g(0) = -2$ , musi zachodzić $f(0) = 0$ . Nie ma informacji, że $f(0) = 0$ , więc odpowiedź D nie musi być prawdziwa.

Wnioski

Po analizie odpowiedzi okazuje się, że prawidłowa odpwiedź to odpowiedź A.